Math Vocabulary: Easy Review

This post has not been fully edited or done.

Triangles

Isosceles

Isosceles is when two sides of a triangle are the same length. To remember this term, you can notice the -sos is the word Isosceles. The s stands for the two sides, which will remind you that an isosceles triangle is a triangle with two equal sides.

Equilateral

Equilateral triangles are when all sides of a triangle are the same length. We can remember this by using the prefix -equal, which can stand for equality. Because the word equal is in the word, we can use this to recognize that an equilateral triangle is a triangle with all the sides in equal length.

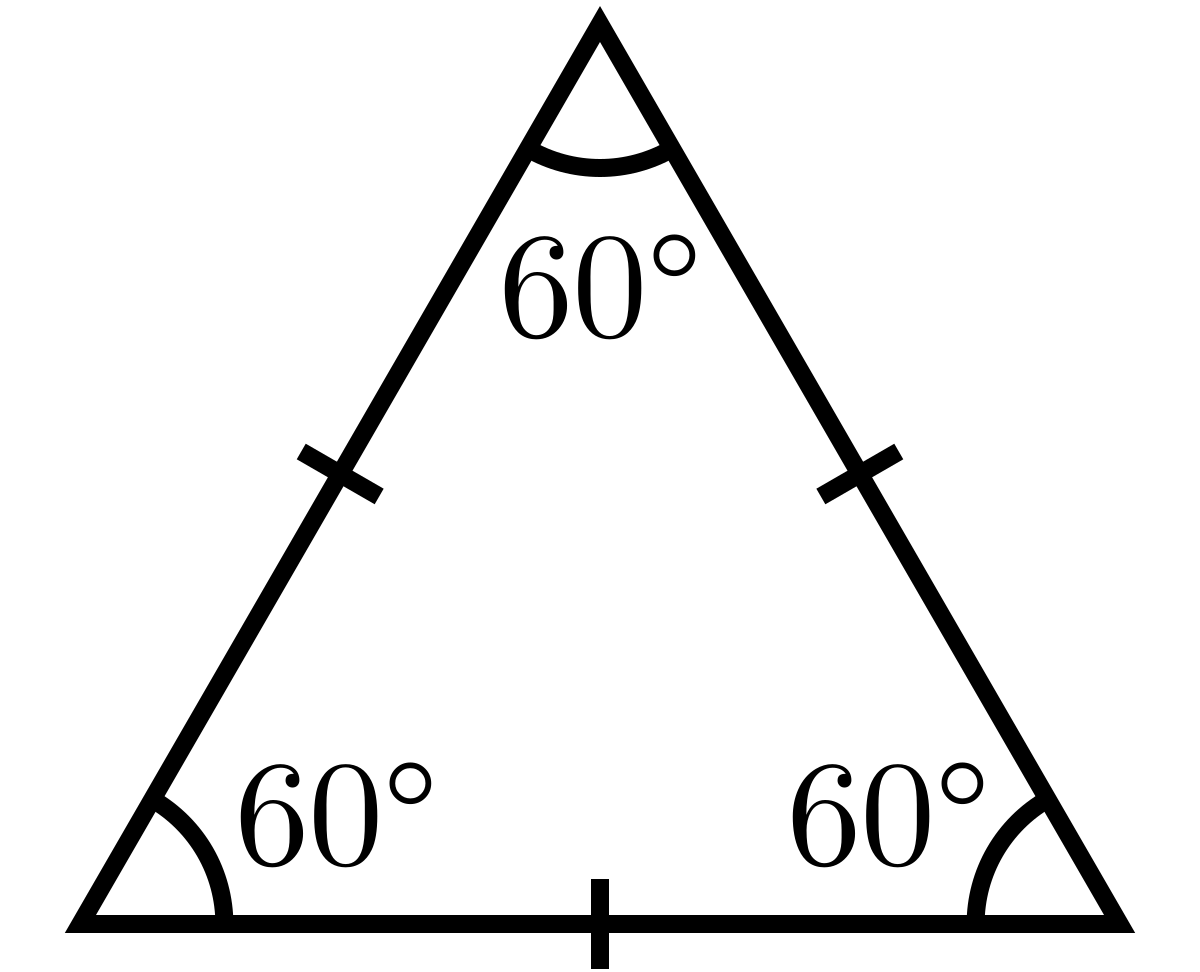
Scalene

With isosceles and equilateral triangles being the first two, it leaves us with scalene. Scalene triangles are when all three sides are of different lengths. We can already infer this since there are no more possible combinations of possibility. (Either all sides are equal, different, or two sides are the same.)

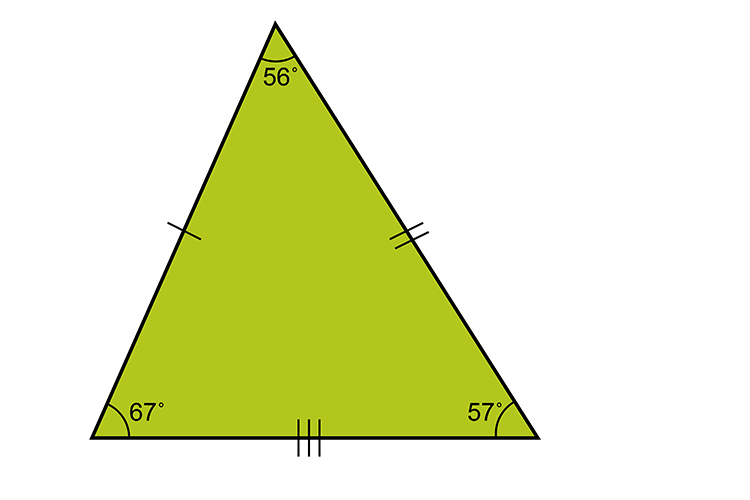
Angles

Acute

An acute angle is an angle that is less than 90 degrees. A 90-degree angle is an angle that stands straight up from a horizontal line. If the angle is measured lower than 90 degrees, then it is called an acute angle. We can also tell if it is an acute angle by the way it looks. If it is slanted toward the right more than it is upright, then it is going to be acute.

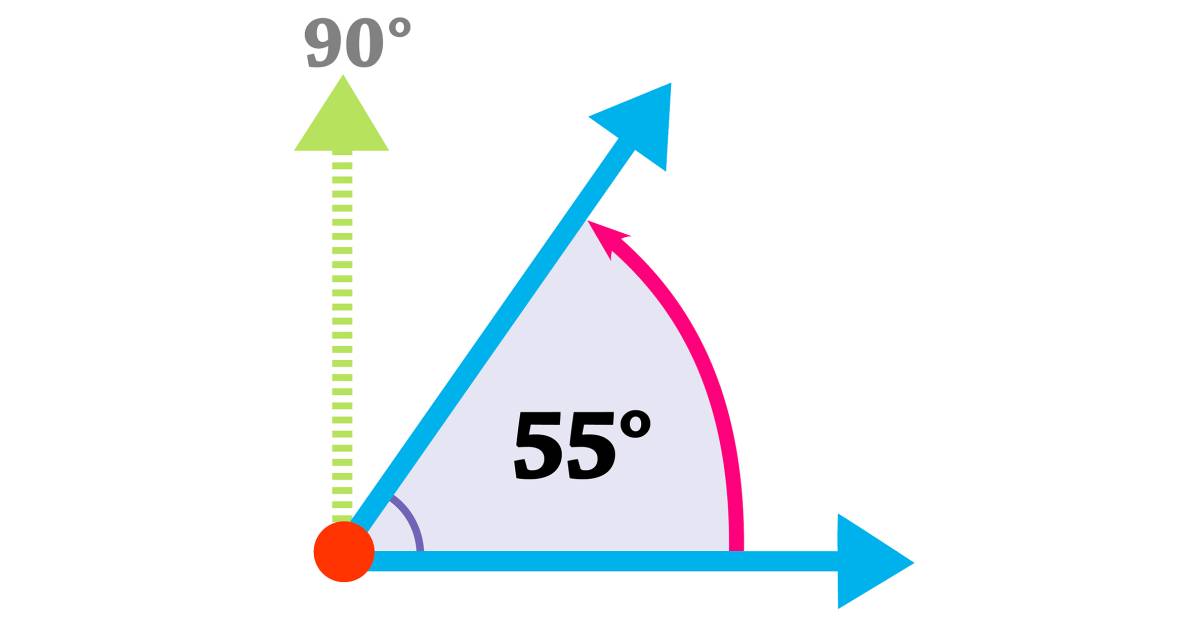
Obtuse

An obtuse angle is an angle that is greater than 90 degrees, but less than 180. An angle of 180 degrees forms a straight line, so a straight line cannot be obtuse. So since an obtuse angle can be greater than 90 degrees but less than 180, possible measurements for the angle could be: 91 degrees, 100 degrees, 179 degrees, and 80 degrees. When there is an obtuse angle in a triangle, there can only be one angle that is greater than 90.

Right

A right angle is an angle that is exactly 90 degrees, not bigger or smaller than 90 degrees, exactly 90. Usually, there is a small cube on the angle to indicate that it is 90 degrees as seen here.

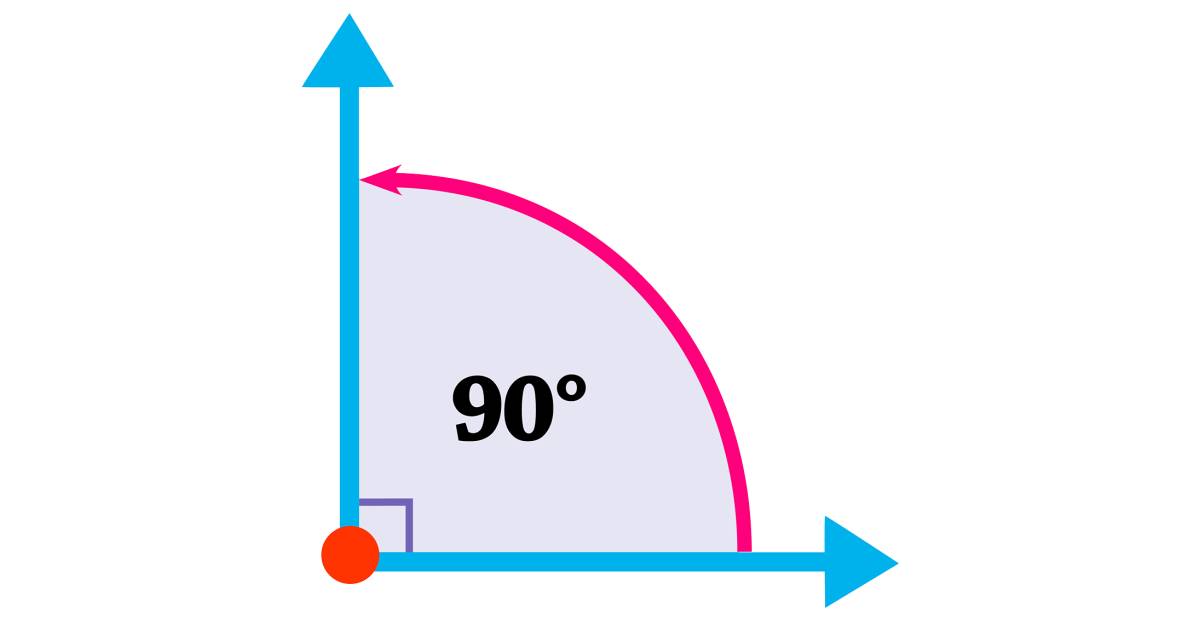
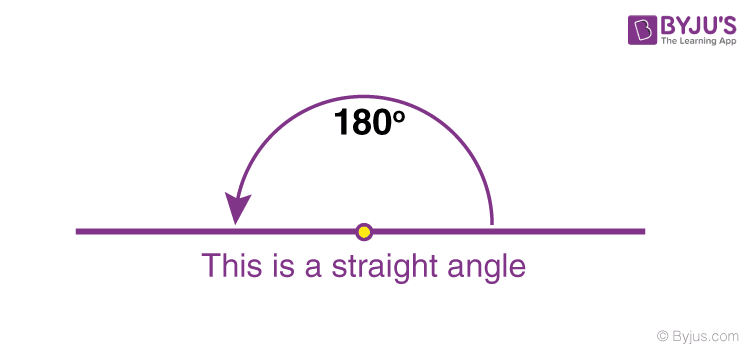
Straight Angle

Like mentioned before, a straight angle is an angle that measures 180 degrees. This forms a straight angle, like its name.

Reflex Angle

A reflex angle is the angle around an angle. It has to be more than 180, but less than 380 degrees. Here is a picture for you to understand.

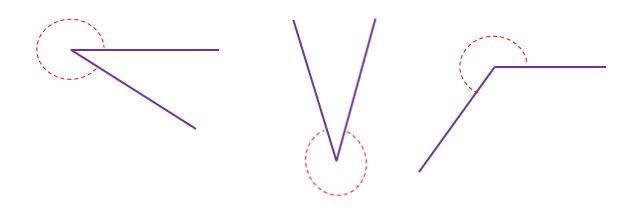
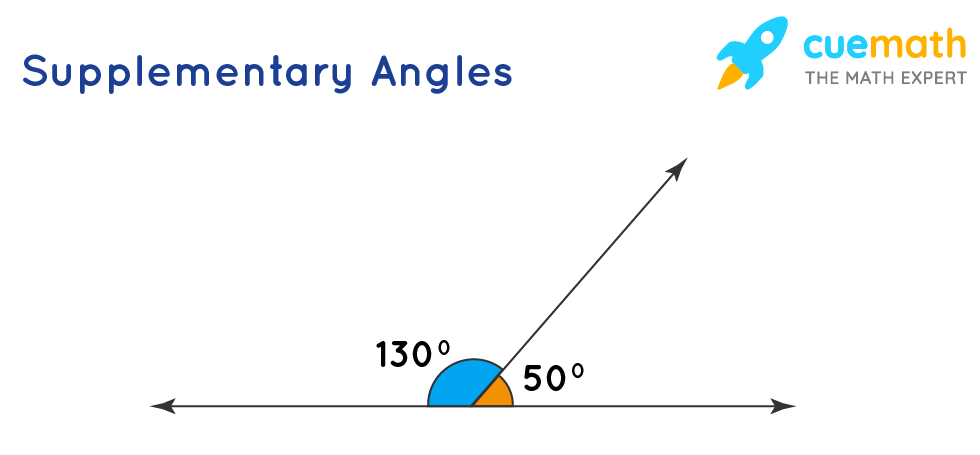
Supplementary

Supplementary angles are angles that add up to 180 degrees. Remember, 180 is a line. To remember what a supplementary angle is, you notice that there is an s in the beginning of the word. The s can stand for the s in straight, which can represent a straight line. the straight line is 180 degrees, so supplementary angles will add up to 180 degrees.

Complementary

Complementary angles are angles that add up to 90 degrees. To remember what a complementary angle is, you can use the first letter of the word, c, and turn it into a 9 with a line. In case you are confused, here is a picture to showcase this trick.

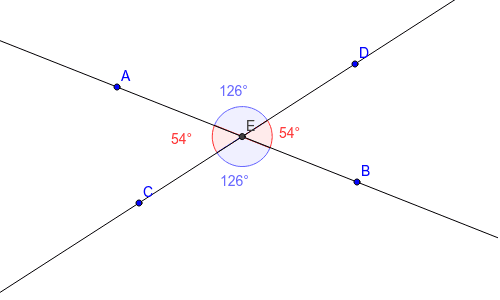
Vertical Angles

Vertical Angles are angles that are vertical (or opposite) of each other and have the same angle. They are made by intersecting lines. For example, if we cut a circle into quarters, (four parts), then we would have four 90 degree angles. The first piece of the circle in the picture shown below has the same angle as the fourth angle. Both of them have an angle of 90 degrees. This is called a vertical angle. When solving questions like these, make sure to calculate the other angles of the lines and intersections as well, for sometimes angles appear to be vertical when being unequal.

Shapes

Congruent Figures

Two shapes are congruent if they share the same size and shape. Their angles and sides are equal to the other as well. To illustrate this, here is a picture of two congruent figures. However, the shape can be translated, rotated, and reflected, which I will talk about on the following paragraph.

Translation

When a shape is translated, it is moved. Not reshaped, rotated, or anything else, just moved. Each of the points of the shape must be moved the same distance and direction. If each corner of a shape is moved 5 spaces, then it is a translated. But if the shape is inverted in the process, then it is not a translated shape. When you take the original shape and the translated shape, you will get congruent figures because the size, angles, sides, and shape did not change.

Rotation

Rotation is the turning of a shape. The size, angle, sides, and shape cannot be changed, but as long as it is rotated and nothing else, then it is going to be congruent to the original shape. To tell whether not or not a shape qualifies as a rotational shape, you can visualize the distance from the original center of the shape and compare it to the “rotational” shape. If the distance is the same, then the shape is a rotated shape and is congruent.

Reflection

Reflection is the inverted filter of a shape. This means that the shape is almost flipped in a way. This means a reflected upright figure will be upside down. The points from the two congruent shapes must be the same distance from the central line. The central line is the line that separates the two shapes. To make this simpler, here is a picture for you to understand better. The mirror line can be in any direction, left, right, upside down, and mostly common: straight.

Notes: Translation, Rotation, and Reflection are all examples of transformations, which is what we call these three congruent changes of shapes.

Numbers

Integers

Integers are whole numbers. They can be positive, negative, or zero. They cannot be decimals or fractions. Examples of integers are: 1, 0 33, 5,900 Non-examples of integers are: 3.14159…., -5.9, 10/9.

Prime Numbers

Prime numbers are numbers that can only be divided by themselves and one. So, it will have only two divisors. This means that 1 is not a prime number, since it can only be divided by one multiple: itself. 0 is not a prime number either. Examples of prime numbers are 2, 3, 5, 7, 9, 11. Non-examples of prime numbers: 4 (can be divided by 2, 1, and 4), and 8 (can be divided by 1,2, 4, and 8)

Irrational Numbers

Irrational numbers are numbers that cannot be written as a ratio or fraction. This means they never stop. You have heard of pi, which is the number 3.14159265358979323….. The digits are ongoing. Fractions aren’t irrational because fractions are basically ratios, which breaks the meaning of irrational numbers. When an irrational number times a rational number is multiplied, it will be a irrational number. This is the same if you multiply a irrational number times a irrational number: you would get an irrational number as well.

Rational Numbers

Rational numbers are numbers that can be made by two integers. This also means that rational numbers can be written as a fraction. For example, 1.5 can be written as 1 5/10 or 1 1/2, which makes it a rational number, not an irrational number, which cannot be written as a fraction. Examples of rational numbers are 3.5, 6.908, 12.56, 5, and 1/9. Examples of irrational numbers are: the square root of 2 and pi (3.14159…)

IMPORTANT: The bottom of rational number’s fraction cannot be 0.