This post has not been fully edited or done. Triangles Isosceles Isosceles is when two sides of a triangle are the same length. To remember this term, you can notice the -sos is the word Isosceles. The s stands for the two sides, which will remind you that an isosceles triangle is a triangle with two equal sides. Equilateral Equilateral triangles are when all sides of a triangle are the same length. We can remember this by using the prefix -equal, which can stand for equality. Because the word equal is in the word, we can use this to recognize that an equilateral triangle is a triangle with all the sides in equal length. Scalene With isosceles and equilateral triangles being the first two, it leaves us with scalene. Scalene triangles are when all three sides are of different lengths. We can already infer this since there are no more possible combinations of possibility. (Either all sides are equal, different, or two sides are the same.) Angles ...
Math
How to learn math effectively, faster, and comprehensively: (Apps, Tips, Answers, and etc. )
Key Idea Where to start off? Well, the first thing I must say about learning math is to learn it well. When I say learning it well, I don't mean learning it the basic way: I mean learning the way that is the most understandable. Many teachers can make things hard to understand and can hinder the way the students learn and process information. The easiest way to learn is to find simple explanations for harder topics. You can find these on YouTube. I highly recommend looking at this channel >https://www.youtube.com/channel/UCEWpbFLzoYGPfuWUMFPSaoA. The Original Chemistry Teacher explains not only math but codes and science as well. They make the videos simple and very easy to understand. Many have learned things that were taught in 2 hours, just by a short 10-minute video. I have learned many things, including polynomials, the quadratic equation and how it is used, and binary code conversion. One of the reasons why some schools students are doing better than others is ...
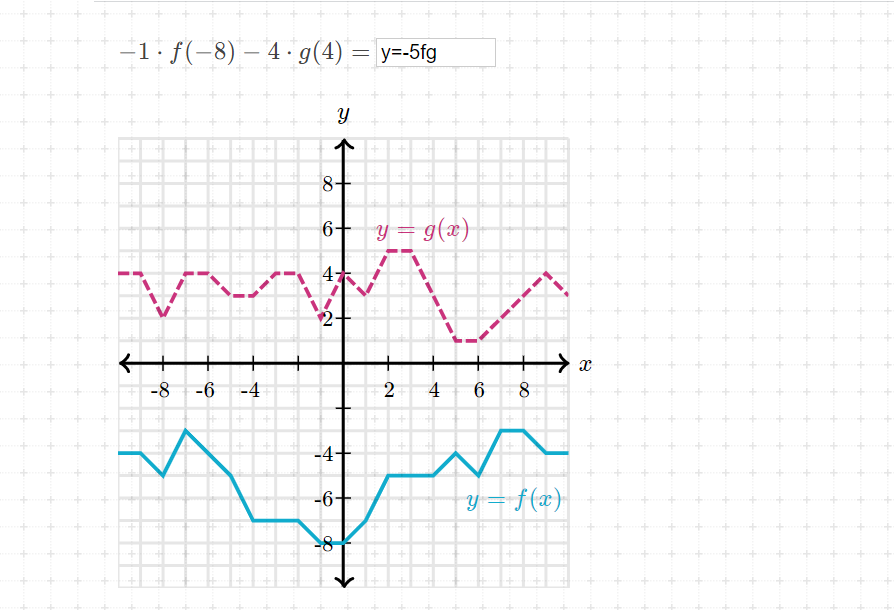
Input and Output Values: How to find Inputs and Outputs on a Graph
(Ignore the answer put into the box, this was when I first was inputs and outputs, and I was totally wrong :D ) At first glance, you may think this seems very complicated, right? Actually, this is a very easy thing to understand. Today, I will be showing you how to indicate inputs and outputs on a graph! :D At you can see this equation is quite long. To make things more simple, let's remove some properties. Our new equation: f(-8) x g(4)=? To first solve this, we must know what a input and output is. A input is something that is put in. For example, when ordering groceries, your input would be your money. A output is a result of a input. Since your input is the money, your output would be your groceries. It is almost like a cause and effect, but in math terms! Now that we know that an input and output is, lets look at the picture. There are two crooked lines: one in red and the other in blue. The red has a equation of y=g(x) and the blue has an equation of y=f(x). You ...
Introduction to Algebra 1: Identify Inequalities, Equations, and Expressions
Before getting into one and two step inequalities, let's first understand what they are. If you have read my other posts, you would know that equations have equal signs, whereas expressions do not. To learn more visit: http://skynotes.steveyan.com/algebraic-expressions/ Algebraic Expressions Equations: Post coming soon. First, let's test your knowledge. Which of these is an inequality? A: 2x+7-9 B: 5x≥ 90 C: 3=x-4=8 If you answered B, ding ding! That's correct. Now, you may have just guessed, so I'll explain how it it is an inequality furthermore. These symbols: ≥ ≤ might make you go, "What?" These symbols are actually very easy to understand. You have probably seen these symbols: ><. These mean greater or less than. The first two symbols look exactly the same, but with a line under them. The line stands for, "equal." When writing x<5 or x is less than 5, x cannot be equal to 5 because it is exactly equal to 5. But with this symbol, ≤ ...
Making equivalent expressions using distributive property and GCF: Understand how to find the GCF in a set of numbers
Well, what is a GCF? GCF acrostically stands for the greatest common factor and is found when listing the factors of a number. A factor is a number that can be multiplied by another to get a number. For example, the number twelve, (12), consists of the factors 1,2,3,4,6, and 12. 1 times 12 equals 12, 2 times 6 also equals 12, as well as 3 times 4. These are called factor pairs. In order to find the GCF, we need a set of numbers. Let's start off with the two numbers 14 and 49. Before I explain, use the explanation in the paragraph above to attempt the question. Before we find the GCF, we need to list out the factors of 14 and 49. 14: 1,2,7,14 49: 1,7,49 Look at the factors of the two numbers and see what they have in common. Have you found the common factor? If you found that 7 was in both sets, then great! This concludes that 7 is the GCF. Now that you know about the GCF, it's time to create an equivalent with distributive concepts. Let's take the expression ...
Dependent and Independent Variables
Before we explain the definition of the dependent and independent variable, let's test your knowledge! Lyla commits to head outside 8 times as much as she spends indoor. X symbolizes the amount of time spent indoor, whereas y symbolizes the time spent outdoors. y=8x Identify the dependent variable in the equation. If you guessed y, you're correct! But do you know why y is the dependent variable? Y is the dependent variable because the value of it changes because of x. Let's say Lyla spent 5 hours indoors. Because she spent 5 hours indoors, the amount of time spent outside would result because of the decision. Think of it as a cause and effect. The cause would be the value of x, which shifts the value of y. In summary, y acts as a result of a decision/value. Too confusing? Here's a definition from google.com: The independent variable is the cause... Its value is independent of other variables in your study. The dependent variable is the effect. ...
HOW TO SIMPLIFY ALGEBRAIC EQUATIONS WITH LIKE TERMS: ADDITION AND SUBTRATION
Intro 2+5+x-7+x When you see this equation, you may be confused. What should I add? How do I add? What's the answer?... I can help you answer the first question. The first thing that may stand out to you are the two variables, x. If you're guessing that we are going to add them, bingo! Well, how do we add them together? We can add them easily, since x=1x. You may be wondering where the 1 popped up. There is actually an 'invisible' 1 hiding in the x! Remember: 1 times any number equals the same number, therefore the value of x will not be affected by multiplying 1. Now, why can't we add 2 plus x? We can't add them because the two are not like terms. If we try adding them together, it would be 2x, which does not make sense, since 2x= x+x, not 2+x. Before we add the two x's together, let's move the variables to one side and the digits on the other. Before: 2+5+x-7+x After: 2+5-7+x+x Question: How did we move all the digits on one side? We moved -7 or negative ...
How to solve basic algebraic equations with the properties of equality: Multiplication and Division
When you see the equation you'd probably know what the answer is. But the real question is, do you know how to show how you got your answer? Remember: Our goal is to get y on one side and numbers and operations on the others. Let's look at the equation. We need to get rid of ÷3 and one way to get rid of it is by doing the inverse operation, multiplication! y÷3=4 ×m So since we multiplied 3, we have moved y to one side and removed ÷3. But, we still have to do one more thing. Do you remember the math rule with equations and expressions? We have to also multiply the 3 to 4! y÷3=4 ×m ×m We have now gotten y on one side, removed ÷3 by multiplying 3 itself, and did the same to 4. In summary, our equation has now simplified into y=12. Let's plugin our answer into the equation! 12÷3=4 Yup! Our answer is correct. We can check by multiplying 3 and 4, which does equal 12. Make sure to always plugin your answer and check! Now that you solved a division ...
How to solve basic algebraic equations with the properties of equality: Addition and Subtraction
When you first see x-4=8, you might instantly know the answer. But do you know how to show how you got your answer? Let's look at the equation. We want to have x on one side and all the other numbers and operations on the other side. Now, this may sound a little confusing, so I'll explain further. We want to get rid of the -4 in x-4=8 so that we can immediately have our answer, x= something. We can't have -4 in the way because x-4=8 is not giving us the answer. So in order to get rid of the -4, we have to use the inverse operation, addition. x-4=8 +4 Now, if we add +4 to the equation, we have x=8. This answer is obviously not correct, for 8-4 does not equal 8. The reason the answer is not correct is because we have not added +4 to 8. Why do we have to add +4 to 8? There is a rule when dealing with equation. Whatever you do on one side, you also have to do on the opposite side. So in this case, we have to add 4 to 8 because we have added 4 to -4. x-4=8 ...
Algebraic Expressions
You may have heard of a numerical expression, but have you heard of a algebraic expression? Numerical and algebraic expressions both have numbers and operations, but algebraic expressions include one more thing, variables. Variables are numbers that are written down as a symbol. You probably heard of x, y, a, c, and etcetera, which are all letters from the alphabet. Variables do not have to be letters, although they are more common. A star could also be a variable. These letters are used a placeholder for varying expressions and quantities, which is why they are called a variable. A algebraic has at least one or more variables. IMPORTANT: Keep in mind that both numerical and algebraic equations DO NOT have equal signs. When a group of numbers and operations do have a equal sign, they are called a equation. Now, let's test your knowledge before we get on to the more complicated information. What type of expression is this? 2+4+1 1. ...